공부한 것
- LeetCode #215. Kth Largest Element in an ArrayKth Largest Element in an Array - LeetCodeCan you solve this real interview question? Kth Largest Element in an Array - Given an integer array nums and an integer k, return the kth largest element in the array. Note that it is the kth largest element in the sorted order, not the kth distinct element. Can you solve it without sorting? Example 1: Input: nums = [3,2,1,5,6,4], k = 2 Output: 5 Example 2: Input: nums = [3,2,3,1,2,4,5,5,6], k = 4 Output: 4 Constraints: * 1 <= k <= nums.length <= 105 * -104 <= nums[i] <= 104
https://leetcode.com/problems/kth-largest-element-in-an-array/description/

⇒ 주어진 숫자 배열에서 k번째로 큰 수를 찾아 반환하는 문제. 수들은 중복으로 존재할 수 있고, sort 함수를 사용하지 말 것.
생각 과정: ‘max heap을 만들어서 k개로 자르고 맨 마지막 수를 반환하기? 안된다. 맨 앞의 수를 제외한 뒤의 수들은 크기 정렬이 안 되어 있다. 그러면 min heap을 만들어서 k개로 자르고 맨 앞의 수를 반환하자.’
1번 풀이 코드:
function findKthLargest(nums: number[], k: number): number { const minHeap: MinHeap = new MinHeap(); for (const num of nums) { // 1. k개에 못 미치면 그냥 넣기 // 2. k개이고 지금 넣는 수가 min보다 크거나 같으면면: min을 먼저 빼고, 지금 수를 넣기 if (minHeap.getLength() < k) minHeap.insert(num); else if (num >= minHeap.getMin()) { minHeap.popMin(); minHeap.insert(num); } } return minHeap.getMin(); }; class MinHeap { private heap: number[]; constructor() { this.heap = []; } // heap배열의 마지막 자리에 위치한 요소를 제자리로(Heapify): bubble up private bubbleUp() { let index = this.heap.length - 1; let element, parentIndex, parent; while (index > 0) { element = this.heap[index] parentIndex = Math.floor((index - 1) / 2); parent = this.heap[parentIndex]; if (element >= parent) break; this.heap[parentIndex] = element; this.heap[index] = parent; index = parentIndex; } } // heap배열의 첫 자리에 위치한 요소를 제자리로(Heapify): bubble down private bubbleDown() { let index = 0; let element: number; let leftChildIndex: number, rightChildIndex: number; let leftChild: number, rightChild: number; let swapTarget: null | number; while (true) { swapTarget = null; element = this.heap[index]; leftChildIndex = index * 2 + 1; rightChildIndex = index * 2 + 2; if (leftChildIndex < this.heap.length) { leftChild = this.heap[leftChildIndex]; if (leftChild < element) { swapTarget = leftChildIndex; } } if (rightChildIndex < this.heap.length) { rightChild = this.heap[rightChildIndex]; if ((swapTarget === null && rightChild < element) || (swapTarget && rightChild < leftChild)) { swapTarget = rightChildIndex; } } if (swapTarget === null) break; this.heap[index] = this.heap[swapTarget]; this.heap[swapTarget] = element; index = swapTarget; } } // 요소를 삽입 insert(num: number) { this.heap.push(num); this.bubbleUp(); } // 최소 요소 추출 popMin() { const min = this.heap[0]; const end = this.heap.pop(); if (this.heap.length > 0) { this.heap[0] = end; this.bubbleDown(); } return min; } getMin() { return this.heap[0]; } getLength() { return this.heap.length; } }
2번 풀이 코드:
function findKthLargest2(nums: number[], k: number): number { nums.sort((a, b) => b - a); // 내림차순 정렬 return nums[k - 1]; }
실행 결과:
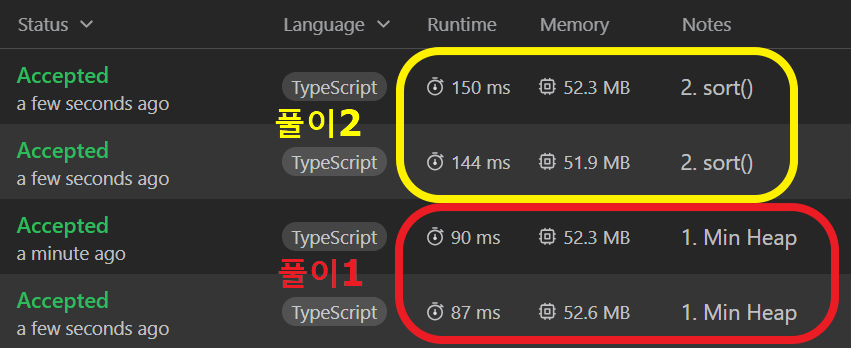
⇒ sort 메소드를 이용한 풀이 2번과 굳이 비교해보니, Min Heap을 이용하는 풀이 1번이 조금 더 빠름을 알 수 있다. sort()는 시간복잡도가 O()이고, Heap은 숫자가 들어올 때마다 logN을 진행해야 하므로 O()이 된다. 두 함수의 크기를 비교하면 다음과 같다:
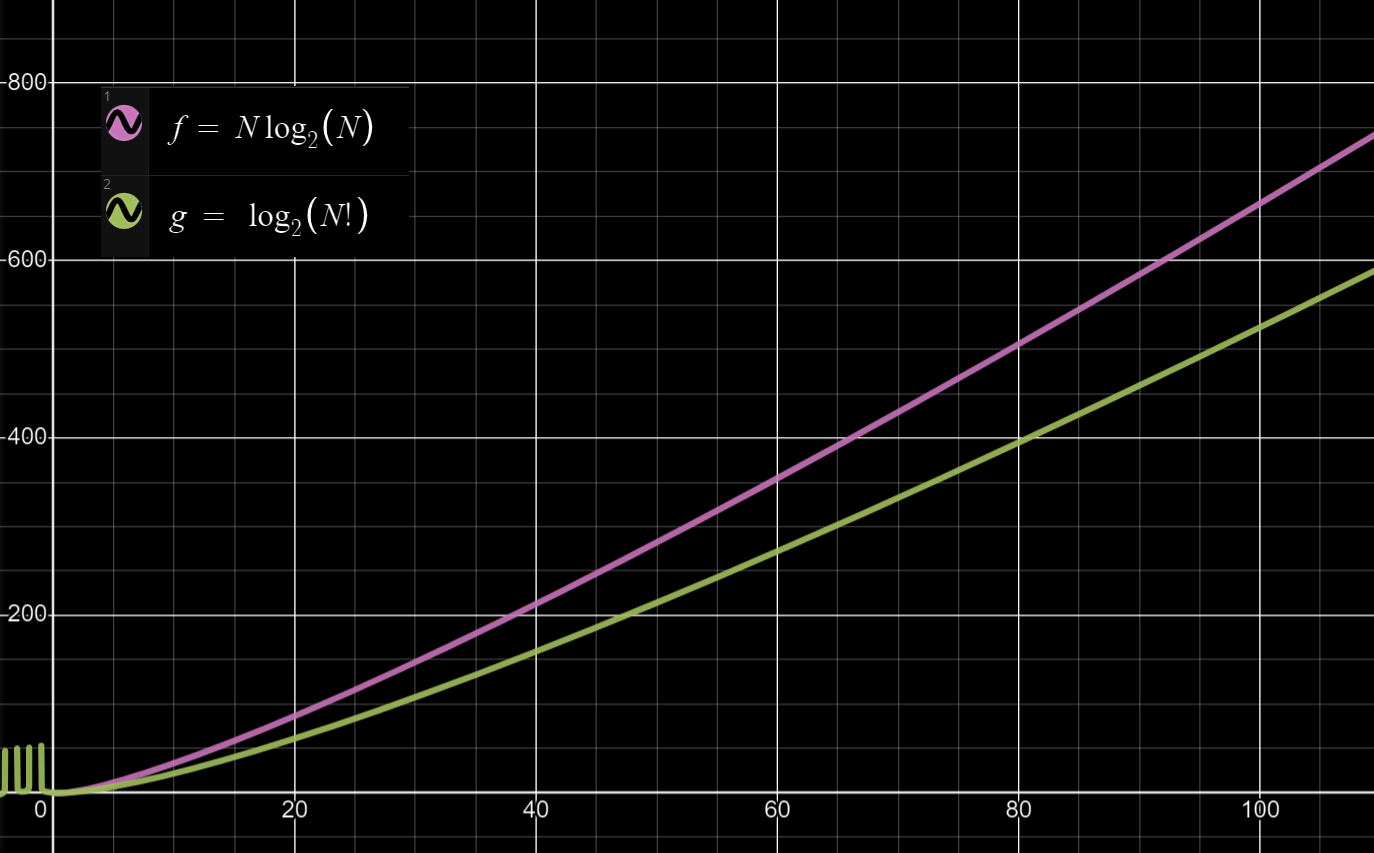
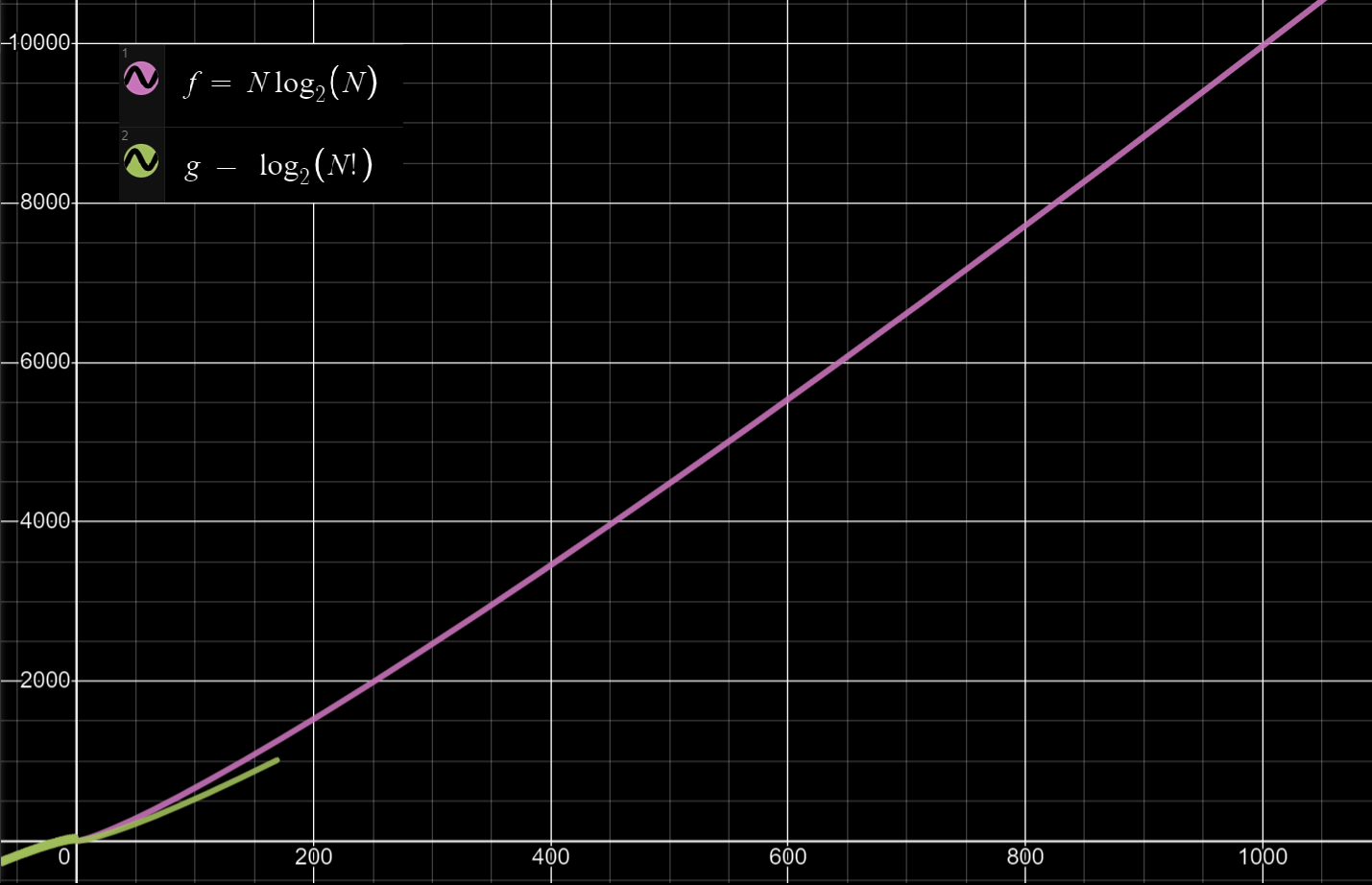
엄청난 차이는 없지만 NlogN 쪽이 더 오랜 시간이 걸린다는 것을 알 수 있다. Min Heap을 이용하는 쪽이 조금 더 빠르며, ‘현재 최소값보다 더 작은 수가 들어올 때는 해당 logN 과정을 생략’할 수도 있음을 생각해볼 때 조금 더 차이가 발생하게 된다. 그래서 위와 같은 실행 시간 차이가 발생하게 된 것이다.
- 최소 힙(Min Heap)을 스스로 구현해 보았다. 어제 기억이 살아 있어서 수월했다.
Uploaded by N2T