공부한 것
- LeetCode #703. Kth Largest Element in a StreamLeetCode - The World's Leading Online Programming Learning PlatformLevel up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
https://leetcode.com/problems/kth-largest-element-in-a-stream/description/

자바스크립트의 sort()을 이용한 풀이와 최소 힙(Min Heap)을 구현해서 푼 풀이의 결과 차이가 엄청나다:
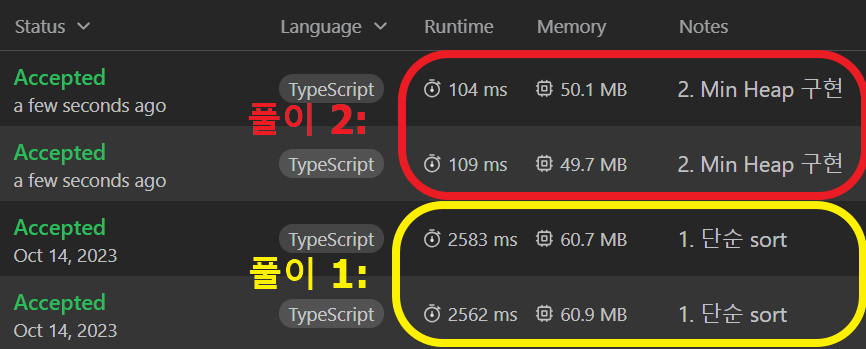
- 번 풀이: add() 호출마다 Array.sort 사용. 초기 nums 길이를 N, add()를 호출하는 횟수를 M이라고 할 때 시간복잡도는 대략 = , 공간복잡도는 이 된다.
코드:
// 배열의 sort() 함수를 이용한 클래스: class KthLargest1 { k: number; heap: number[]; constructor(k: number, nums: number[]) { this.k = k; this.heap = []; for (const num of nums) { this.add(num); } } // Time complexity: O(N log N) + O(N) => O(N log N + N) // Space complexity: O(log N) add(val: number): number { // 힙에 요소를 추가하고 오름차순 정렬 this.heap.push(val); this.heap.sort((a, b) => a - b); // 크기를 k로 제한 if (this.heap.length > this.k) { this.heap.shift(); } // k번째로 큰 요소 반환 return this.heap[0]; } }
- 번 풀이: 매 add() 호출마다 전체 배열을 정렬하지 않고, 배열 길이를 k로 제한한 상태에서 최소 힙을 이용해 최소값만 빠르게 제일 앞으로 옮기는 방식을 통해 시간복잡도를 획기적으로 줄였다. 시간복잡도: , 공간복잡도: .
코드:
//^ 최소 힙(Min Heap)을 구현하여 KthLargest에 활용하기: // => 매 add() 호출마다 전체 배열을 정렬하지 않고, 배열 길이를 k로 제한한 상태에서 최소 힙을 이용해 최소값만 빠르게 제일 앞으로 옮기는 방식을 통해 시간복잡도를 획기적으로 줄였다. class MinHeap { private heap: number[]; constructor() { this.heap = []; } //^ 삽입한 요소를 힙 구조에 맞게 위치 조정(heapify) - Bubble up // Time complexity: O(log N) // Space complexity: O(1) private bubbleUp() { // 마지막 요소에서 시작. 부모와 교체할 때마다 그 위치로 index 값이 조정됨. 그렇게 업데이트되는 바뀌는 위치가 root 노드에 도달하기까지 아래 루프를 반복한다. let index = this.heap.length - 1; while (index > 0) { // 해당 요소의 부모 노드 위치를 계산해서 그 값을 parent로 지정한다. heap은 왼쪽부터 꽉꽉 채워서 차례로 들어가는 반 완전 이진 트리(?)로 본다. const element = this.heap[index]; const parentIndex = Math.floor((index - 1) / 2); const parent = this.heap[parentIndex]; // 새로 삽입한 요소와 부모 노드를 비교하여 위치를 조정: // 만약 지금 요소가 부모보다 크거나 같으면 전체 루프를 멈춘다. if (element >= parent) break; // 만약 부모보다 값이 작으면 자리를 바꾼다. this.heap[index] = parent; this.heap[parentIndex] = element; // (부모와 바꿔서) 새롭게 위치한 자리를 새로운 index로 삼는다. index = parentIndex; // 자신보다 작은 부모를 만나거나 루트에 도달하기까지 과정을 반복한다. } } //^ 추출한 요소를 힙 구조에 맞게 위치 조정(heapify) - Bubble Down // Time complexity: O(log N) // Space complexity: O(1) private bubbleDown() { // 앞의 요소부터 시작한다. let index = 0; const element = this.heap[index]; // 무한 루프를 돌면서 while (true) { // 현재 요소의 두 자식 위치를 구한다. const leftChildIndex = index * 2 + 1; const rightChildIndex = index * 2 + 2; let leftChild, rightChild; let swapTarget = null; // 각 자식마다, 자식의 위치가 실제 존재하는 노드라면(=heap의 길이 내라면) 그 값을 leftChild, rightChild에 저장한다. 또 각 자식이 현재 요소보다 작으면 자리를 바꿔야 하므로, 바꿀 타겟이 되는 위치 변수 swapTarget에 자식의 위치를 따로 저장한다. if (leftChildIndex < this.heap.length) { leftChild = this.heap[leftChildIndex]; if (leftChild < element) { swapTarget = leftChildIndex; } } // 그래서 만약 "왼 자식은 그대로 두고 오른 자식만 바꿔야 하든지", "왼 자식도 바꿔야 하는데 오른 자식이 왼보다 더 작다면(더 작은 쪽을 위로 올려야 하므로)" 오른 자식을 바꿀 대상 swapTarget으로 삼는다. if (rightChildIndex < this.heap.length) { rightChild = this.heap[rightChildIndex]; if ((!swapTarget && rightChild < element) || (swapTarget && rightChild < leftChild)) { swapTarget = rightChildIndex; } } // 교체할 대상이 없다면 현재 루프를 break한다. 루프 전체에서 break하는 부분이 여기뿐으로, 두 자식 중 더이상 바꿀 대상이 없는 경우에만 무한 루프를 멈추게 된다. if (!swapTarget) break; // 교체할 대상이 있다면 현재 노드와 교체한다. this.heap[index] = this.heap[swapTarget]; this.heap[swapTarget] = element; // 다시 '현재 요소'의 위치를 바꾼 타겟 위치로 지정하고 루프를 계속한다. index = swapTarget; } } //^ 요소를 삽입 // Time & Space complexity: bubbleUp()과 동일 insert(value: number) { // heap배열의 마지막에 요소를 삽입하고, 알맞은 위치로 찾아가도록 this.bubbleUp() 활용 this.heap.push(value); this.bubbleUp(); } //^ 최소 요소 추출 // Time & Space complexity: bubbleDown()과 동일 popMin() { // 제일 앞의 요소가 반환 대상이다.(아직 안뽑음) const min = this.heap[0]; // 제일 뒤의 요소를 뽑고서(?) 만약 heap이 비게 됐다면 이게 곧 반환할 최소값이라는 소리이므로 그대로 반환한다. const end = this.heap.pop(); // 만약 heap 길이가 아직 0이 아니면 뽑은 수를 제일 앞 자리로 덮어씌워준다. 그리고 거기서부터 bubbleDown해서 제자리를 찾도록 한다. if (this.heap.length > 0) { this.heap[0] = end; this.bubbleDown(); } return min; } //^ 힙의 길이를 반환 getLength() { return this.heap.length; } //^ 최소값을 반환(추출 없이) getMin() { return this.heap[0]; } } //^ 최소 힙(클래스 MinHeap)을 이용하는 KthLargest 클래스 class KthLargest { private k: number; private minHeap: MinHeap; //^ 초기화 // Time complexity: O(N log N) // Space complexity: O(N) constructor(k: number, nums: number[]) { this.k = k; this.minHeap = new MinHeap(); // 초기 배열 nums를 최소 힙에 넣어주기 for (const num of nums) { // this.minHeap.insert(num); this.add(num); } } //^ 요소 추가 및 K번째로 큰 요소 반환 // Time complexity: O(log N) // Space complexity: O(1) add(value: number): number { //~ 시나리오1: 현재 최소 힙 길이가 k에 미치지 못하는 경우: 단순히 최소 힙에 삽입시켜준다. 그 후 힙의 최소값을 반환한다. if (this.minHeap.getLength() < this.k) { // O(log N) this.minHeap.insert(value); return this.minHeap.getMin(); } // 현재 최소 힙 길이가 k인 경우(더 클 수는 없다): else { // O(1) //~ 시나리오2: 넣으려는 값이 힙의 최소값보다 작으면 k번째로 큰 순위에 영향을 미치지 못할 것이므로, 힙에서 빼거나 더하지 않고 현재 힙의 최소값을 반환한다. if (value < this.minHeap.getMin()) return this.minHeap.getMin(); //~ 시나리오3: 넣으려는 값이 힙의 최소값보다 크거나 같으면 순위 변동이 생긴다: 먼저 힙에서 최소값을 추출하고, 새 요소를 넣어준다. 그 후 힙의 최소값을 반환한다. else { // O(2 log N) this.minHeap.popMin(); this.minHeap.insert(value); return this.minHeap.getMin(); } } } }
따라서 두 풀이는 대략 MN과 M+N만큼의 시간차가 발생한다. 예를 들어 초기 nums길이가 100개, add() 호출을 100번 했다고 하면 각각 10,000과 200에 비례하도록 실행시간이 달라지게 된다.
+ 추가: 그런데 계산이 잘 맞지 않는다. 두 풀이에서 add()에 sort를 사용하는가와 최소 힙을 사용하는가에 따라 대략 O(N log(N))과 O(log(N))의 차이가 발생한다고만 생각해야겠다.
- 번 풀이: add() 호출마다 Array.sort 사용. 초기 nums 길이를 N, add()를 호출하는 횟수를 M이라고 할 때 시간복잡도는 대략 = , 공간복잡도는 이 된다.
- 우선순위 큐(Priority Queue):
: 각 요소에 우선순위를 할당하고 각 우선 순위에 따라 요소들을 정렬하거나 관리하는 자료구조. 요소를 삽입하거나 제거할 때마다 최소/최대 우선순위 요소를 큐의 맨 앞에 위치시키는 원리이다.
- 우선순위 큐가 사용되는 상황들:
- 작업 스케줄링: 각 작업에 우선순위를 할당하고 가장 높은 우선순위를 갖는 작업을 가장 먼저 처리한다.

출처: “Priority Queue Pattern” - https://learn.microsoft.com/en-us/azure/architecture/patterns/priority-queue 
참고: “CPU Process Scheduling Algorithms in OS” - https://www.allbca.com/2020/04/cpu-process-scheduling-algorithms-in-os.html 
참고: “Priority Scheduling Algorithm in Operating System” - https://prepinsta.com/operating-systems/priority-scheduling-algorithm/
- 다익스트라 알고리즘: 최단 경로를 찾을 때, 다음에 방문할 노드를 선택하기 위해 최단 거리에 따라 정점을 관리한다. Dijkstra 다익스트라 알고리즘 정리Dijkstra 다익스트라 알고리즘 공부한 것을 기록으로 남깁니다.
 https://v3.leedo.me/devs/69
https://v3.leedo.me/devs/69
- 힙 정렬: 요소들을 힙에 삽입한 다음 루트를 추출하여 정렬된 순서로 반환한다.
- 작업 스케줄링: 각 작업에 우선순위를 할당하고 가장 높은 우선순위를 갖는 작업을 가장 먼저 처리한다.
- 우선순위 큐가 사용되는 상황들:
Uploaded by N2T