9/5 (화) 재귀함수와 백트래킹 TIL

공부한 것

오늘은 재귀함수에 대한 유튜브 강의를 듣다가 백트래킹(Backtracking)이라는 용어가 나오길래 정확히 어떤 건지 궁금하여 찾아보았다.

백트래킹(Backtracking, 퇴각검색)

길이 여러 갈래로 나뉘어진 재귀호출이다. 가능한 모든 경우의 수를 낱낱이 탐색할 때 사용한다.

주로 다음과 같은 경우에 백트래킹을 적용한다:

• 일정한 크기의 조건들이 주어지고, 그 안에서 완전탐색을 통해 최적비용 또는 최적경로를 탐색해야 하는 경우.

• 각 조건에서 선택할 수 있는 경우의 수가 정해져 있을 경우 (이차원 배열 등)

예제 1) 주사위 던지기

: 주사위를 N개 던져서 나올 수 있는 경우의 수를 모두 출력하기

• 코드:

  // 주사위를 N번 던진 결과의 모든 조합을 배열 형태로 출력하기.
  // 예를 들어 3번 던진 결과는 [1,1,1],[1,1,2]... 이렇게 나올 수 있다. 
  
  // 1. 변수 선언 및 초기화
  const N = 3;
  const result: number[] = [];
  // 2. 재귀함수 호출
  roll(0);
  
  function roll(diceNum: number) {
  	// 3. 탈출조건(Base condition)
  	if (diceNum === N) { // N번 주사위를 던지면 탈출.
  		console.log(result);
  		return;
  	}
  	// 4. 경로 탐색
  	for (let i = 1; i <= 6; i++) {
  		result[diceNum] = i;
  		diceNum++;
  		roll(diceNum); // diceNum이 0부터 N까지 되도록 
  		diceNum--;
  		result[diceNum] = 0; // 이 줄은 없어도 동일하게 동작한다.
  	}
  }
  
  // 결과: 
  [1, 1, 1]
  [1, 1, 2]
  [1, 1, 3]
  [1, 1, 4]
  [1, 1, 5]
  [1, 1, 6]
  [1, 2, 1]
  [1, 2, 2]
  [1, 2, 3]
  [1, 2, 4]
  ...

예제 2) 주사위 던지기 II

: 주사위를 던져서 모두 다른 수가 나오는 경우를 출력하기. [1,2,3]과 [1,3,2]를 같은 경우로 간주하여 하나만 출력해야 한다.

아래 세 가지 해답은 모두 동일한 정답을 출력한다:

• 현재 완성시키고 있는 조합을 저장할 전역 배열과 중복을 검사할 Set을 활용하는 해답:

  function IWantToThrowDice3Times() {
  	// const N = parseInt(prompt("How many rolls: ")); // node.js에서는 활용 불가
  	const N = 3;
  	const resultCombination: Array<number> = [];
  	const usedCombinations = new Set<String>();
  
  	throwDice(0);
  
  	function throwDice(currentRoll: number) {
  		if (resultCombination.length === N) {
  			const sortedResult = [...result].sort((a, b) => a - b);
  			const combinationString = JSON.stringify(sortedResult);
  
  			// '이미 등장한 조합'에 포함되지 않는 조합만 새로 등록하고 출력 
  			if (!usedCombinations.has(combinationString)) {
  				usedCombinations.add(combinationString);
  				console.log(resultCombination);
  			}
  			return;
  		}
  
  		for (let i = 1; i <= 6; i++) {
  			resultCombination.push(i);
  			throwDice(currentRoll + 1);
  			resultCombination.pop();
  		}
  	}
  }
  
  IWantToThrowDice3Times();

• Set을 제거한 해답: for문으로 반복하는 숫자 자체를 제한한다.

  function IWantToThrowDice3Times2() {
  	const N = 3;
  	const resultCombination: Array<number> = [];
  
  	throwDice(0);
  
  	function throwDice(currentRoll: number) {
  		if (resultCombination.length === N) {
  			console.log(resultCombination);
  			return;
  		}
  
  		for (let i = (resultCombination.length > 0 ? resultCombination[resultCombination.length - 1] : 0) + 1; i <= 6; i++) {
  			// 중복되지 않는 숫자인 경우
  			resultCombination.push(i);
  			throwDice(currentRoll + 1);
  			resultCombination.pop();
  		}
  	}
  }
  
  IWantToThrowDice3Times2();

• 전역 배열도 제거한 해답: 전역 변수 resultCombination을 매개변수로 이동한다.

  function IWantToThrowDice3Times3() {
  	const N = 3;
  
  	throwDice(0, []);
  
  	function throwDice(currentRoll: number, resultCombination: number[]) {
  		if (resultCombination.length === N) {
  			console.log(resultCombination);
  			return;
  		}
  
  		for (let i = (resultCombination.length > 0 ? resultCombination[resultCombination.length - 1] : 0) + 1; i <= 6; i++) {
  			// 중복되지 않는 숫자인 경우
  			resultCombination.push(i);
  			throwDice(currentRoll + 1, resultCombination);
  			resultCombination.pop();
  		}
  	}
  }
  
  IWantToThrowDice3Times3();

예제 3) N-Rooks

: N*N크기의 체스판에 N개의 룩을 배치하되, 서로 경로가 겹치지 않도록 배치하는 경우의 수를 모두 찾기.

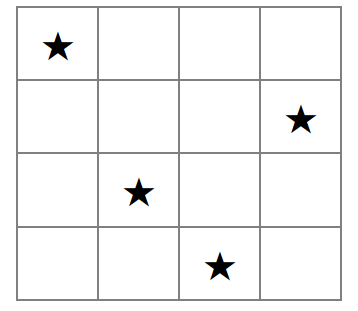
핵심 로직: 행(row)이 다 닳으면 반복을 탈출하고(탈출조건) 열(col)이 이미 방문한 곳이면 다시 가지 않는다(경로탐색).

• 코드:

  function findRooks() {
  	// 1. 변수 선언 및 초기화
  	let N: number; 				// 체스 보드 크기 N
  	let map: number[][];		// 체스코드 배열, 룩의 위치를 나타냄
  	let visited: number[];		// 열 방문 여부를 나타내는 배열
  
  	N = 4;
  	map = new Array(N).fill(0).map(() => new Array(N).fill(0));
  	visited = new Array(N).fill(0);
  	let row = 0;
  
  	// 2. 재귀 함수 호출
  	locate(row); // 행별로 룩을 재귀적으로 배치(0번째 행부터 N-1번째 행까지)
  
  	function locate(row: number) {
  		// 3. 탈출 조건(Base condition)
  		if (row === N) { // 모든 행에 룩을 배치한 경우
  			printResult();
  			return;
  		}
  		// 4. 경로 탐색
  		for (let col = 0; col < N; col++) {
  			if (visited[col] !== 1) { // 현재 열이 방문되지 않은 경우
  				map[row][col] = 1; // 해당 위치에 룩을 배치
  				visited[col] = 1;  // 해당 열을 방문 표시
  
  				locate(row + 1); // 다음 행으로 이동하여 룩 배치를 계속함
  
  				visited[col] = 0; // 배치를 원래대로 되돌림(Backtracking)
  				map[row][col] = 0;
  			}
  		}
  	}
  
  	function printResult() {
  		for (let i = 0; i < N; i++) {
  			console.log(map[i]); // 현재 상태의 체스보드를 0부터 N줄까지 행별로 출력
  		}
  		console.log("----------------"); // ----로 체스보드를 구분함.
  	}
  }
  
  findRooks();
  /* 실행 결과: 
  [ 1, 0, 0, 0 ]
  [ 0, 1, 0, 0 ]
  [ 0, 0, 1, 0 ]
  [ 0, 0, 0, 1 ]
  ----------------
  [ 1, 0, 0, 0 ]
  [ 0, 1, 0, 0 ]
  [ 0, 0, 0, 1 ]
  [ 0, 0, 1, 0 ]
  ----------------
  ...
  
  ----------------
  [ 0, 0, 0, 1 ]
  [ 0, 0, 1, 0 ]
  [ 1, 0, 0, 0 ]
  [ 0, 1, 0, 0 ]
  ----------------
  [ 0, 0, 0, 1 ]
  [ 0, 0, 1, 0 ]
  [ 0, 1, 0, 0 ]
  [ 1, 0, 0, 0 ]
  ----------------
  */

예제 4) 제한 조건 내의 최소합

: 위 문제의 체스보드에 숫자가 채워져 있다고 할 때, 가능한 룩 배치 조합 중 숫자 합이 최소가 되는 위치 조합을 찾기. 즉, 0~100으로 채워진 NxN의 2차원 행렬 중 열과 행이 겹치지 않는 N개의 숫자를 선택하여 만들 수 있는 최소합 찾기.

15	12	7	8
21	28	15	18
13	11	17	10
24	19	22	15

• 코드:

  function findMinSum() {
  	// 1. 변수 선언 및 초기화
  	let N: number;
  	let map: number[][];
  	let visited: number[];
  	let minSum: number;
  	let selectedNums: number[];
  	let selectedNumsResult: number[];
  
  	N = 4;
  	map = new Array(N).fill([]).map(() => []);
  	visited = new Array(N).fill(0);
  	minSum = Infinity;
  	selectedNums = new Array(N).fill(-1);
  
  	// 임의로 0에서 100까지의 수로 map 배열 초기화
  	for (let i = 0; i < N; i++) {
  		for (let j = 0; j < N; j++) {
  			map[i][j] = Math.floor(Math.random() * 101);
  		}
  	}
  	
  	let row = 0; 
  	let sum = 0;
  	
  	// 2. (현재 행렬과 함께)재귀 함수 호출
  	selectNum(row, sum);
  	printBoard();
  	console.log('열별로 선택된 수: ', selectedNumsResult);
  	console.log('최소합: ', minSum);
  
  	function selectNum(row: number, sum: number) {
  		// 3. 탈출 조건: 행(row)가 끝에 다다르면
  		if (row === N) {
  			if (sum < minSum) { // 이번에 만든 sum이 더 작다면
  				minSum = sum;
  				selectedNumsResult = [...selectedNums];
  			}
  			return;
  		}
  		// 3-5. 가지치기: 끝 행에 다다르지 않았는데 '역대 최소합'을 넘어버리면 이 루트는 버린다
  		if (sum > minSum) return;
  
  		// 4. 경로 탐색
  		for (let col = 0; col < N; col++) {
  			if (visited[col] !== 1) {
  				sum += map[row][col];
  				visited[col] = 1;
  				selectedNums[col] = map[row][col];
  				
  				selectNum(row + 1, sum);
  
  				selectedNums[col] = -1;
  				visited[col] = 0; 
  				sum -= map[row][col];
  			} 
  		}
  	}
  
  	function printBoard() {
  		for (let i = 0; i < N; i++) {
  			console.log(map[i]);
  		}
  		console.log("--------------");
  	}
  }
  
  findMinSum();
  /* 출력 결과: 
  [ 82, 40, 55, 55 ]
  [ 61, 15, 5, 79 ]
  [ 29, 38, 89, 89 ]
  [ 96, 90, 11, 92 ]
  --------------
  행별로 선택된 수:  [ 29, 15, 11, 55 ]
  최소합:  110
  */

예제 5) 음식 주문하기 I (제한 조건 내의 최대합)

: 한정된 예산을 '최대한 모두 사용하여' 음식 주문하기. 한 번 선택한 메뉴는 다시 선택하지 않는다. 즉, 메뉴에 있는 음식 중 예산은 넘어가지 않으면서 가격 총합이 가장 큰, 중복되지 않는 음식 조합 찾기.

음식 이름	가격
치킨	20000
피자	30000
족발	40000
중식	64000
곱창	33000
분식	24000
회	72000

핵심 로직: 합계(sum)가 한계에 닿으면 반복을 탈출하고(탈출조건) 이미 방문한 메뉴면 다시 가지 않는다(경로탐색).

• 코드:

  function findOrderMenu() {
  	// 1. 
  	const MENU: string[] = ["치킨", "피자", "족발", "중식", "곱창", "분식", "회"];
  	const PRICE: number[] = [20000, 30000, 40000, 64000, 33000, 24000, 72000];
  	const LIMIT: number = 200000;
  
  	let visited: number[] = new Array(7).fill(0);
  	let orderList: string[] = [];  // 마지막에 출력할 총 메뉴
  	let totalPrice: number = 0;    // 마지막에 출력할 총 가격
  
  	let tempPrice = 0;				// 가격 합계를 임시저장 
  	let tempOrder: string[] = [];  // 메뉴를 임시저장
  
  	// 2. 재귀합수 호출
  	order(tempPrice, tempOrder);
  
  	console.log('총 주문 가격: ', totalPrice);
  	console.log('총 주문 메뉴: ', orderList);
  
  	function order(tempPrice: number, tempOrder: string[]) {
  		// 3. 탈출 조건(Base condition): 현재까지의 주문 가격이 예산 한도를 넘으면 재귀 호출을 멈추고 메뉴를 더 탐색하지 않는다. 
  		if (tempPrice > LIMIT) {
  			return;
  		}
  		// 3-5. 현재 가격 합계가 합계 최고 기록보다 크면 결과 값 갱신
  		if (tempPrice > totalPrice) {
  			totalPrice = tempPrice;
  			orderList = [...tempOrder];
  		}
  
  		// 4. 경로 탐색
  		for (let i = 0; i < MENU.length; i++) {
  			if (visited[i] === 0) {
  				tempOrder.push(MENU[i]);
  				tempPrice += PRICE[i];
  				visited[i] = 1;
  
  				order(tempPrice, tempOrder);
  
  				visited[i] = 0;
  				tempPrice -= PRICE[i];
  				tempOrder.pop();
  			}
  		}
  	}
  }
  
  findOrderMenu();
  /* 출력 결과: 
  // LIMIT = 150000일 때
  총 주문 가격:  149000
  총 주문 메뉴:  [ '치킨', '곱창', '분식', '회' ]
  
  // LIMIT = 180000일 때
  총 주문 가격:  180000
  총 주문 메뉴:  [ '치킨', '중식', '분식', '회' ]
  
  // LIMIT = 200000일 때
  총 주문 가격:  200000
  총 주문 메뉴:  [ '족발', '중식', '분식', '회' ]
  */

예제 6) 음식 주문하기 II (제한 조건 내의 최대합)

: 한정된 예산 내에서 만족도가 최대가 되도록 조합한 메뉴와 그 때의 가격, 만족도를 출력하기.

음식 이름	가격	만족도
치킨	20000	100
피자	30000	150
족발	40000	190
중식	64000	250
곱창	33000	200
분식	24000	120
회	73000	300

• 코드:

  function findMaxSatisfyingMenu() {
  	// 1. 
  	type TMenuElement = {
  		[key: string]: {
  			price: number,
  			satisfaction: number,
  		},
  	}
  	
  	const MENU: TMenuElement = {
  		치킨: { price: 20000, satisfaction: 100 },
  		피자: { price: 30000, satisfaction: 150 },
  		족발: { price: 40000, satisfaction: 190 },
  		중식: { price: 64000, satisfaction: 250 },
  		곱창: { price: 33000, satisfaction: 200 },
  		분식: { price: 24000, satisfaction: 120 },
  		회: { price: 73000, satisfaction: 300 },
  	}
  	const LIMIT: number = 73000;
  
  	let maxSatisfaction: number = 0;  // 출력할 최종 만족도
  	let totalPrice: number = 0; 	  // 출력할 최종 가격 합
  	let finalOrder: string[] = [];	  // 출력할 최종 메뉴
  
  	let visited: Set<String> = new Set();   // 방문한 메뉴
  	let tempSatisfaction: number = 0;		// 만족도를 임시 저장
  	let tempPrice: number = 0; 				// 가격 총합을 임시 저장
  	let tempOrder: string[] = []; 			// 메뉴를 임시 저장
  
  	// 2. 재귀함수 호출
  	order(tempPrice, tempSatisfaction, tempOrder);
  
  	console.log('총 만족도: ', maxSatisfaction);
  	console.log('총 주문 가격: ', totalPrice);
  	console.log('총 주문 메뉴: ', finalOrder);
  
  	function order(tempPrice: number, tempSatisfaction: number, tempOrder: string[]) {
  		// 3. 탈출 조건(Base condition) 
  		if (tempPrice > LIMIT) {
  			return;
  		}
  
  		if (tempSatisfaction > maxSatisfaction) {
  			maxSatisfaction = tempSatisfaction;
  			totalPrice = tempPrice;
  			finalOrder = [...tempOrder];
  		}
  
  		// 4. 경로 탐색
  		for (let [menu, { price, satisfaction }] of Object.entries(MENU)) {
  			if (!visited.has(menu)) {
  				tempOrder.push(menu);
  				tempPrice += price;
  				tempSatisfaction += satisfaction;
  				visited.add(menu);
  
  				order(tempPrice, tempSatisfaction, tempOrder);
  
  				visited.delete(menu);
  				tempSatisfaction -= satisfaction;
  				tempPrice -= price;
  				tempOrder.pop();
  			}
  		}
  	}
  }
  findMaxSatisfyingMenu();
  /* 출력 결과: 
  // LIMIT = 50000
  총 만족도:  250
  총 주문 가격:  50000
  총 주문 메뉴:  [ '치킨', '피자' ]
  
  // LIMIT = 73000
  총 만족도:  390
  총 주문 가격:  73000
  총 주문 메뉴:  [ '족발', '곱창' ]
  
  // LIMIT = 200000
  	// 가격 기준으로 맞췄을 때:
  		총 주문 가격:  200000
  		총 주문 메뉴:  [ '족발', '중식', '분식', '회' ]
  	// 만족도 기준으로 맞췄을 때:
  		총 만족도:  960
  		총 주문 가격:  200000
  		총 주문 메뉴:  [ '피자', '족발', '곱창', '분식', '회' ]
  */

---

백트래킹 예제 참고한 곳: https://wikidocs.net/125659

재귀함수에 대한 짧은 유튜브 시리즈: https://www.youtube.com/watch?v=twuC1F6gLI8&list=PLgUwDviBIf0rGlzIn_7rsaR2FQ5e6ZOL9&index=4

Uploaded by N2T